Function f(x) is a continuous function defined for all real values of x, such that f(x) = 0 only for two distinct real values of x. It is also known that

• f(6) + f(8) = 0
• f(7).f(9) > 0
• f(6).f(10) < 0
• f(0) > 0 and
• f(1) < 0

How many of the following statements must be true?

I. f(1).f(2).f(3) < 0

II. f(3).f(5).f(7).f(9) > 0

III. f(7).f(8) < 0

IV. f(0) + f(1) + f(9) + f(10) > 0

(a) 1 (b) 2 (c) 3 (d) 4

OA : Official Answer – (B)

Solution : f(0) > 0 and f(1) < 0 implies that one root for f(x) = 0 lies between x = 0 and x = 1.

f(6) + f(8) = 0 implies that f(6) and f(8) are of opposite sign but same absolute value. Hence another root for f(x) = 0 must lie between x = 6 and x = 8. As f(1) < 0, f(6) must also be less than zero, otherwise we’ll have more than 2 roots for f(x) = 0.

Hence f(8) > 0 and f(6) < 0.

Further f(7).f(9) > 0 implies that both f(7) and f(9) are greater than zero. So the second root for f(x) = 0 must lie between x = 6 and x=7

So f(x) would look like :

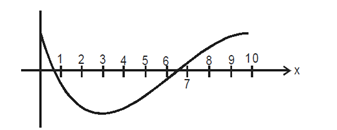
As f(1), f(2) and f(3) are less than zero, f(1).f(2).f(3) < 0 is true.

As f(3), f(5) < 0 and f(7), f(9) > 0, f(3).f(5).f(7).f(9) > 0 is true.

As f(7), f(8) > 0, f(7).f(8) < 0 is false.

f(0), f(9), f(10) > 0 and f(1) < 0, but since we don’t know the magnitude of any of these four we cannot judge if f(0) + f(1) + f(9) + f(10) is greater than zero or not.

To Enrol in CAT MBA Preparation Courses : Visit www.azucation.org.in or

To Join Online Classroom Coaching – Visit Azucation / 3e Learning – Ranchi Center – Click Here to Know The Location